how to find cross sectional area

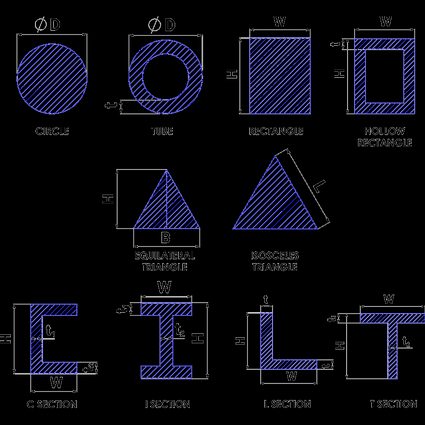
A cross-section is defined as the common region obtained from the intersection of a plane with a 3D object. For instance, consider a long circular tube cut (intersect) with a plane. You'll see a couple of concentric circles. The concentric circles are the cross-section of a tube. Similarly, the beams — L, I, C, and T — are named based on the cross-section shape.

Section view of a Tube

In order to calculate the area of a cross-section, you need to look at them as basic shapes. For instance, a tube is a concentric circle. Therefore, for a tube with inner and outer diameter (d and D) having thickness t, the area of cross-section can be written as:

A_C = π * (D² - d²) / 4

We also know that the inner diameter d is related to thickness t and outer diameter D as:

d = D - 2 * t

Therefore, the area of cross-section becomes:

A_C = π * (D² - (D - 2 * t)²) / 4

Similarly, the area of cross-section for all other shapes having width W, height H, and thicknesses t₁ and t₂ are given in the table below.

Cross-sections

Section	Area
Hollow Rectangle	(H * W) - ((W - 2t₁) * (W - 2t₂))
Rectangle	W * H
I	2 * W * t₁ + (H - 2 * t₁) * t₂
C	2 * W * t₁ + (H - 2 * t₁) * t₂
T	W * t₁ + (H - t₁) * t₂
L	W * t + (H - t) * t
Isosceles Triangle	0.5 * B * H
Equilateral Triangle	0.4330 * L²
Circle	0.25 * π * D²
Tube	0.25 * π (D² - (D - 2 t)²)